はじめましての方ははじめまして。
ほかの記事から来た方はいつもありがとうございます。
qwertです。
『バスケットボール』というスポーツを知っているだろうか?
オリンピックにも採用されている有名なスポーツの一つだ。Wikipediaによると、”1891年にアメリカで考案されたスポーツ。5人対5人の2チームが、一つのボールを手で扱い、長方形のコート上の両端に設置された高さ305cm(10ft)、直径45cm(18in)のリング状のバスケットにボールを上方から通すこと(ゴール)で得点を競う球技である。”(リンク) 攻守が目まぐるしく変わるスポーツで、審判が笛を吹くまで選手を動きっぱなしといっても過言ではない。
漫画だと『スラムダンク』『あひるの空』『黒子のバスケ』が有名。
ゴールを狙う際、オフェンス(攻める側)はいかにディフェンス(守る側)を引き離すかを考える。そんな中、確実に目の前にディフェンスがいない状態でシュートを打てる場合がある。
それがフリースローだ。
シュート中に反則(例えば、手をたたく、体を押すなど)があった場合、フリースローラインからのシュートができる。ノーマークのため、プロなら基本百発百中である。(邪魔できるとしたら、集中を散らすため手を動かしたり、あるいは敵側のサポーターが観客席から変な動きをしたりである)
しかして、実際百発百中を達成するために、果たしてどれくらいの誤差が許されるのだろう?
これについて、物理してみる。
前提条件
まずは条件を明確化しておく。
・コートの規定はJBA公式の競技規則(2019年時点)に則る
・ゴールは前述したように、高さ305cmで径45cmとする
・ボールは質量608.5g、直径24.5cmとする
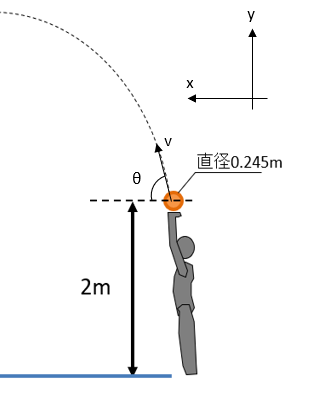
・シュート打点は200cmとする
身長170cmで手を伸ばすと大体このくらいとなるだろう
図で表すと下のようになる。
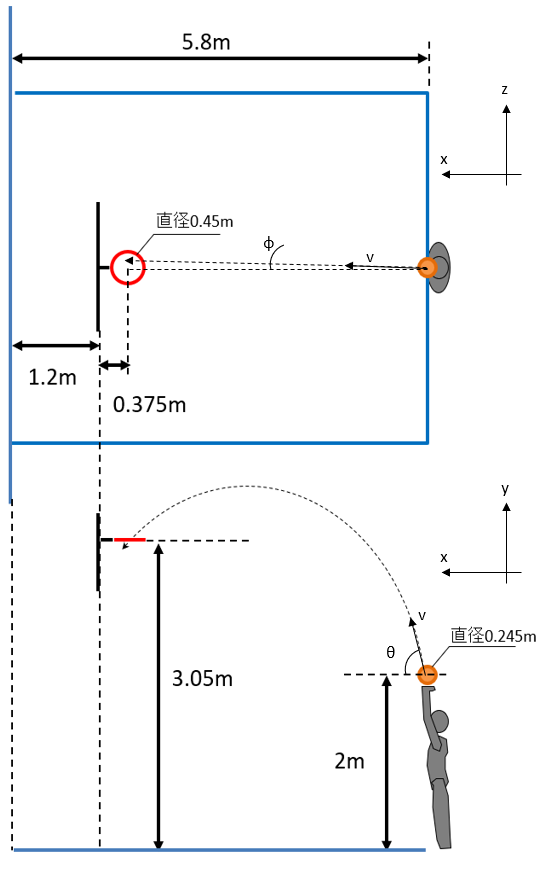
また、
・空気抵抗、ボールの回転による力は無視する
・バックボード使ったシュートではなく、直接リングに入れるシュートを考える
・リングはシュート2秒後に通過とする。
・シュート時力を加えている時間は0.2秒とする
基本式導出
運動方程式を考えて、ボールにかける力とボールの投射角でシュート成功に許される範囲を導出していく。
$$\bf{F}=m\frac{d^2\bf{x}}{dt}$$
Fは ボールにかかる力で F =(Fx,Fy,Fz) 、mはボールの質量、xはボールの位置で3次元表現であり、x =(x,y,z)とする。 tは時間である。 ボールの速度をv=(Vx,Vy,Vz)とし、運動方程式から位置と速度について、各方向で解くと
速度:
$$V_{x}=\frac{F_{x}}{m}t+C_{vx}, V_{y}=\frac{F _{y} }{m}t+C_{vy}, V_{z}=\frac{F_{z}}{m}t+C_{vz}$$
位置:
$$x=\frac{1}{2}\frac{F_{x}}{m}t^2+C_{vx}t+C_{x}, y=\frac{1}{2}\frac{F_{y}}{m}t^2+C_{vy}t+C_{y} , z=\frac{1}{2}\frac{F_{z}}{m}t^2+C_{vz}t+C_{z} $$
となる。Cは定数で、初期条件(t=0の時の条件)を(x,y,z)=(0,0,0)、(Vx,Vy,Vz) =(vcosθcosφ, vsinθcosφ,vsinφ)とする。また、力について、手から離れた瞬間からの運動を考えるため、(Fx,Fy,Fz) =(0, -mg,0)となる。よって、整理すると、
速度:
$$V_{x}=vcosθcosφ,
V_{y}=-gt+ vsinθcosφ ,
V_{z}=vsinφ $$
位置:
$$x= vcosθcosφ t,
y=-\frac{1}{2}gt^2+ vsinθcosφ t ,
z= vsinφ t$$
となる。
ボールが中心を通るとき
ます、簡単なイメージ付けのため、2秒後にボールの中心がリングの中心を通る時を考えてみる。
つまり、
t=2の時:(x,y,z)=( 4.225,1.05,0 )
という条件が追加される。この座標は、上の図から引き算で簡単に算出できる。
代入すると
$$4.225= 2vcosθcosφ ,
1.05=-2g+ 2vsinθcosφ ,
0= 2vsinφ$$
はじめに、z方向の式からφ=oになる。よって、
$$4.225= 2vcosθ, 1.05=-2g+ 2vsinθ$$
gを9.8[m/s^2]で計算すると、
$$vcosθ=2.1125, vsinθ=10.325$$
2つの式から、
$$\frac{vsinθ}{ vcosθ}=tanθ≃4.89 →θ≃78.4°$$
どちらでもいいが、例えばx方向の式から
$$v=10.54[m/s]$$
となる。
力に置き換えるときは、運動量保存の法則を使う。
$$F=\frac{mv’-mv}{Δt}$$
Δtは変化の時間、v’は変化後の速度、vは変化前の速度である。Δt=0.2[s]とすると、
$$F=\frac{ 608.5 ×10^{-3} × 10.54 }{0.2}≃32.9[N]$$
結論、 2秒後にボールの中心がリングの中心を通るには、31.9[N]の力で投射角78.4°でシュートを打てばいいと考えられる。
一般式化
イメージ付けの結果から、やることとしては
・投射角φ,θの取れる範囲を算出
・初速度vをφとθで表して、力Fに直す
になる。
まずφの範囲についてだが、これは図形的に出せる。 つまり、下図の関係から、
$$tan^{-1}(\frac{z_{min}}{x_{nom}})≦φ≦ tan^{-1}(\frac{z_{max}}{x_{nom}}) $$
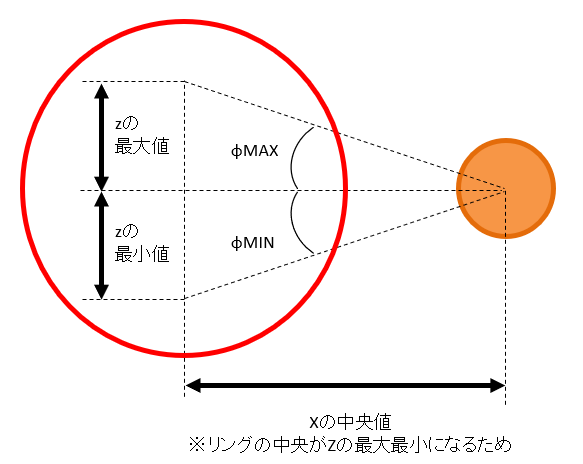
また、t=t0でリング内の点(x0,y0,z0)を通るとすると、位置の式に代入して
$$x_{0} = vcosθcosφ t_{0} ,
y_{0} =-\frac{1}{2}g t_{0} ^2+ vsinθcosφ t_{0} ,
z_{0} = vsinφ t_{0} $$
になる。x方向とy方向の式から
$$tanθ=\frac {y_{0}+\frac{1}{2}gt_{0}^2} {x_{0}}$$
この式から、θの取れる範囲を算出できる。さらに、x方向の式に代入して
$$v= \frac {y_{0}+\frac{1}{2}gt_{0}^2} { tanθsinθcosφ t_{0} }$$
運動量保存の式より
$$F=\frac{mv’-mv}{Δt}= \frac{m}{Δt}
\frac {y_{0}+\frac{1}{2}gt_{0}^2} { tanθsinθcosφ t_{0} } $$
これで、 初速度vをφとθで表して、力Fに直す ことができた。
シュート成功範囲は?
ゴールになるギリギリのポイントを考えると、下図のようにリングにボールが内接しているときで、それよりもリングの中心側にボールの中心が入れば成功になる。
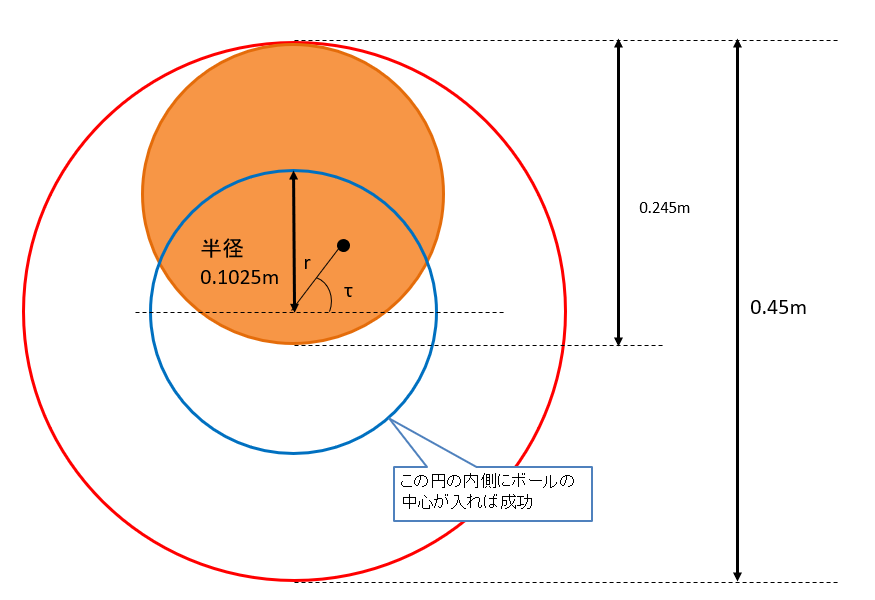
リングを通る瞬間の時間を2秒とすると、
t=2の時: (x0,y0,z0) =(4.225-rcosτ, 1.05, rsinτ), 0≦r≦0.1025, 0≦τ≦360°
がシュート成功の条件となる。
結論
今までの情報から計算すると、φの取れる範囲は
$$-1.39°≦φ≦1.39° $$
θは計算すると、下記に表のようになる。
| τ[°] | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 | 360 |
| x0[m] | 4.1225 | 4.1362 | 4.1738 | 4.2250 | 4.2763 | 4.3138 | 4.3275 | 4.3138 | 4.2763 | 4.2250 | 4.1738 | 4.1362 | 4.1225 |
| tanθ | 5.009 | 4.992 | 4.948 | 4.888 | 4.829 | 4.787 | 4.772 | 4.787 | 4.829 | 4.888 | 4.948 | 4.992 | 5.009 |
| θ[°] | 78.71 | 78.67 | 78.57 | 78.44 | 78.30 | 78.20 | 78.16 | 78.20 | 78.30 | 78.44 | 78.57 | 78.67 | 78.71 |
よって、θの取れる範囲は
$$78.16°≦θ≦78.71°$$
この範囲での初速度vは下記のマップのようになる
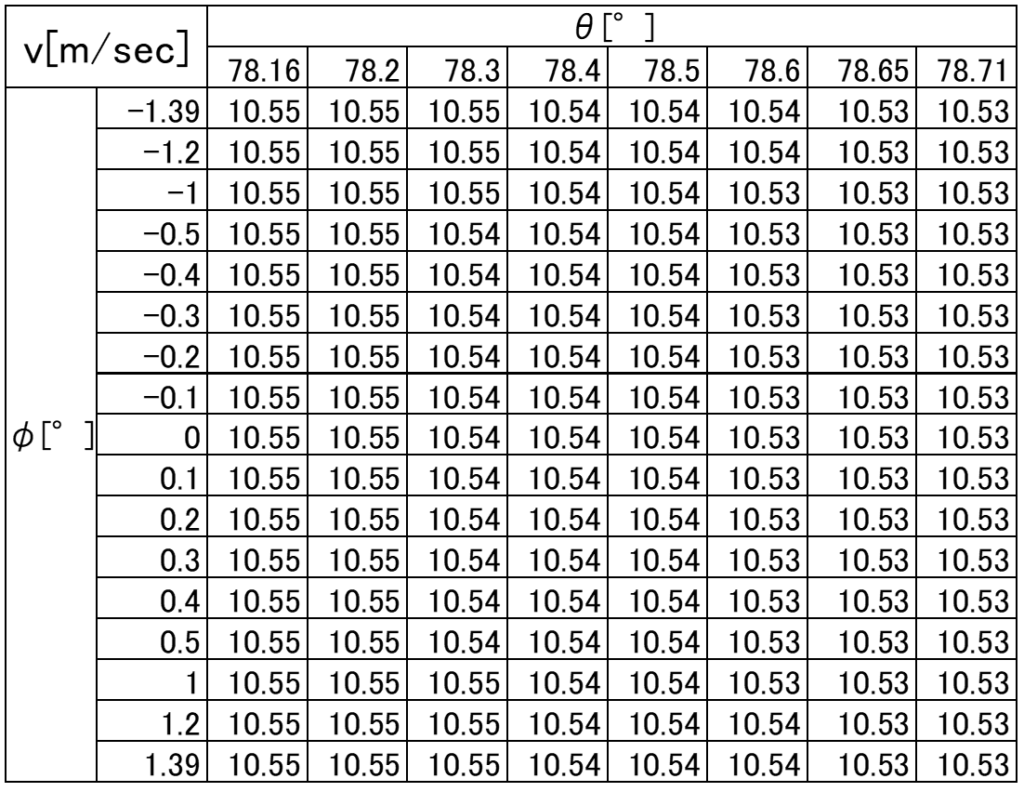
ここで、さらにシュートの成立条件から
$$(x_{0}-4.225)^2+z_{0}^2≦r_{max}^2=0.1025^2$$
となる。vのマップと位置の式から上記の条件を考慮すると、下記マップの黄色の部分が成立することになる。
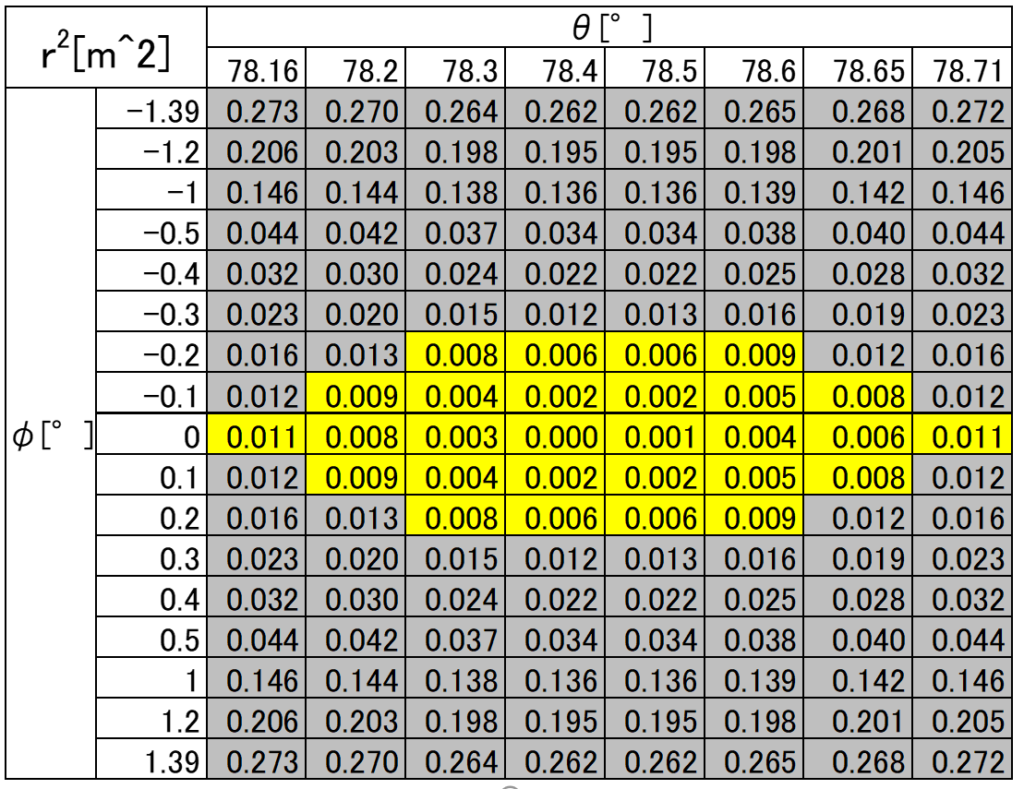
よって、力Fのマップとその成立領域は下のようになる。
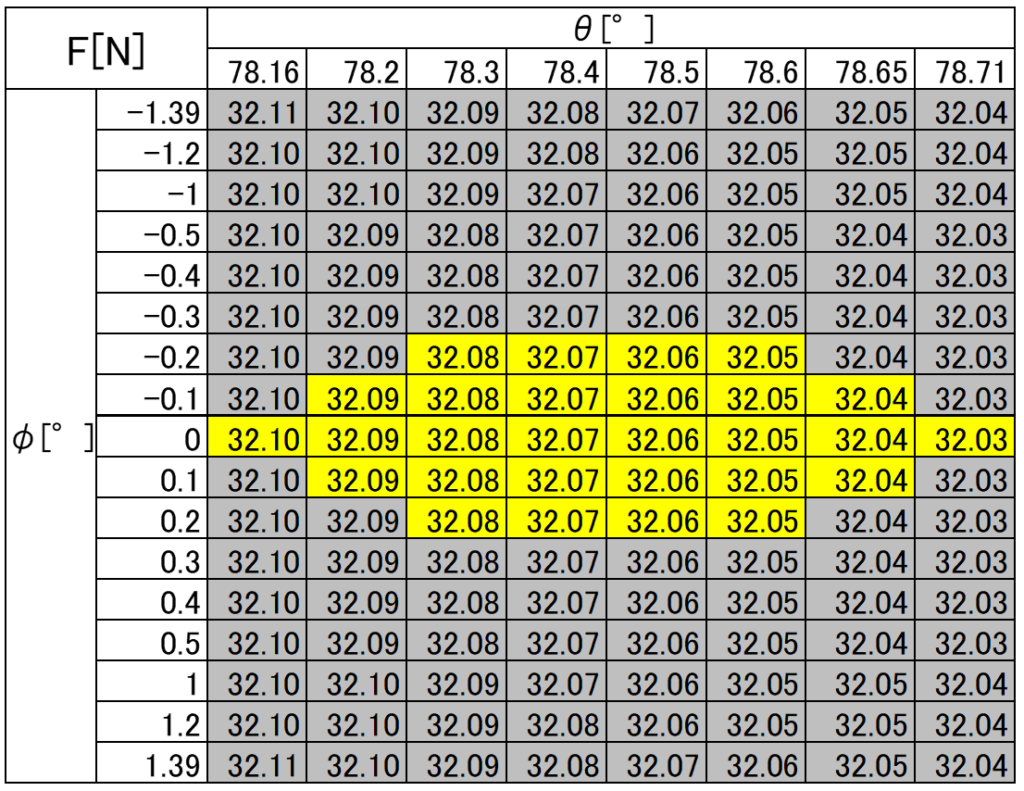
この範囲がフリースローの成立領域と考えられる。
おわりに
かなり範囲が狭く、精密な力加減が必要だということが分かった。さすが習慣のスポーツ。
また、いろいろな前提が置いてあるため、その条件ではこうであるということをゆめゆめ忘れないでほしい。現実には空気抵抗はあるし、バックボードだってある。
時間tも任意の数字でしたかったが、方程式が足らず断念した。いいアイデアがあったら、コメントしてほしい。
最後に、面白いと思っていただけると、幸いで、幸せです。


コメント